The Cycloid

PROBLEM:

Consider a circle of radius a that rolls without sliding along the horizontal x-axis at a constant speed v. We want to find the trajectory traced by a point on the boundary of this circle, as it rolls over the x-axis.

>	with(plots): read "cycloid-figs.mpl";

>	display(fig1);

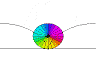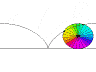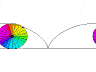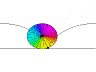
The figure above displays a rolling unit circle at t = 0, t = Pi, and t = 2 Pi. As the circle moves to the right, the blue arrow initially at 6 o'clock, turns around tracing the black archs that form the cycloid. To find out the equation of the cycloid we notice that the position vector at time t, R(t), is given by,

>	R := t -> C(t) + d(t):

where C(t) represents the position vector of the center of the circle at time t,

>	C := t -> v*t*i + a*j:

which encodes the given fact that the center of the circle moves with constant speed v along the x-axis starting from (0,a). Recall that a is the radius of the circle. The blue vector d(t) just turns around the center of the circle. Hence, d(t) is given by:

>	d := t -> a*cos(b-w*t)*i + a*sin(b-w*t)*j:

Clearly d(t) = d(t+T), i.e., it is a periodic function of t with period T obtained from the periodicity of sines and cosines. We find T by,

>	T := solve(b - w*(t+T) = b - w*t - 2*Pi, T);

and since we know that the circle of radius a is rolling at constant speed v along the x-axis, we deduce that it takes,

>	T := 2*Pi*a/v;

units of time to make one complete turn. Thus,

>

w := v/a:

The value of b is chosen so that d(0) = -a j. This requires cos(b) = 0 and sin(b) = -1. Therefore,

>	b := -Pi/2:

and we obtain the vector position funtion for the trajectory of the cycloid as:

>	`R(t)` := collect(R(t),[i,j]);

THE LENGTH OF ONE ARCH OF THE CYCLOID

Clearly the speed v only affects the parametrization but not the resulting curve and we can always assume v = 1. We have,

>	x := t - a*sin(t/a); y := a*(1-cos(t/a));

It is worth noticing that the parametrization can be simplified further by replacing t/a with a new parameter t. This will produce the cannonical form for the cycloid: x = a(t- sin t), y = a(1- cos t). Had we being computing by hand, this would have being a more convenient parametrization to use. But here the computations are not being done by hand so we continue using the previous parametrization where t stands for the usual time in seconds. The components of the velocity vector are then,

>	dx/dt = diff(x,t); dy/dt = diff(y,t);

the speed at time t is then given by the length of the velocity vector. i.e.,

>	ds/dt = sqrt(diff(x,t)^2 + diff(y,t)^2);

the length of one arch is then,

>	L := Int(sqrt(diff(x,t)^2 + diff(y,t)^2),t=0..2*Pi*a);

expanding the square inside the square root we obtain,

and L becomes 8a as it is shown by the following integration,

>	L := Int(sqrt(2)*sqrt(1-cos(t/a)),t=0..2*Pi*a);

>	assume(a>0): L := int(sqrt(2)*sqrt(1-cos(t/a)),t=0..2*Pi*a);

THE AREA UNDER ONE ARCH OF THE CYCLOID

Solving for t in terms of y we get,

>	y := 'y': t := solve(y = a*(1-cos(t/a)),t);

so x as a function of y is given by,

>	x := t - a*sin(t/a);

We compute the area under one arch by adding horizontal stripes for each value of y from 0 to 2a, like in the following figure:

>	display(fig2);

>	Area := 2*Int(Pi*a-x,y=0..2*a);

>	Area := 2*int(Pi*a-x,y=0..2*a);