Pst!, SIR
The SIR model for epidemics is one of the simplest models for contagion processes. It is based on the following three assumptions,
- There are a fixed number \(N\) of individuals.
At each time \(t\), the \(N\) individuals are clasified into three mutually exclusive groups: \((S,I,R)\), thus, \(N=S+I+R\) is constant for all \(t\) but,
\(S=S(t)\) are the number of individuals that at time \(t\) fall into the category of Susceptible individuals. These are the ones that are able to become infected.
\(I=I(t)\) are the Infective individuals at time \(t\), that are able to infect others.
\(R=R(t)\) are the Removed ones. These account for the individuals that die due to the virus or that become inmune after catching the virus.
The basic SIR model is a system of three difference equations for the changes \(\delta S, \delta I, \delta R\). Where for \(U=U(t)\) we define \(\delta U = U(t+1)-U(t)\) so that \(U(t+1) = U(t) + \delta U\) provides the rule to evolve the process from time \(t\) to time \(t+1\). The first equation just says that \(N\) is constant, i.e. \(\delta N =0\), and since \(N=S+I+R\), and the \(\delta\) operation is linear we get,
\[ \delta S + \delta I + \delta R = 0\]
- The second equation specifies the basic nonlinearity of the SIR model. Susceptible individuals can only move into the Infective group by catching the virus from an Infective individual. There are \(S\cdot I\) possible matches and a proportion \(a > 0\) of them will become infected. Thus,
\[ \delta S = -a\cdot (S\cdot I) \]
- The third, and final equation of the SIR model just says that all the changes in Removed come from Infectives either by bocoming inmune after catching the virus, or by dying due to the infection. Therefore, the number of Removed indivuals can only increase by another proportion \(b > 0\) of the Infectives at that time,
\[\delta R = b\cdot I\]
Using the first equation, \(\delta I = -\delta S - \delta R\). Substituting equations (2) and (3) of the SIR model into the right hand side we get,
\[ \delta I = \left(\frac{a}{b}S - 1\right) b \cdot I \]
Notice that since \(b>0\), the Infectives increase (\(\delta I > 0\)), decrease (\(\delta I < 0\)) or stay put (\(\delta I = 0\)), depending on \(R_{0} = a S/b\) being grater than \(1\), or less than \(1\), or equal to \(1\).
Now if we assume that these functions of \(t\) are smooth, we can integrate the last equation. Make \(\delta t\) (which is often \(1\) day) infinitesimally small (one hour, minute,second \(\ldots\)) so that when \(\delta t \rightarrow 0\) the last equation becomes,
\[ \int \, \frac{dI}{I} = \int \left(R_{0}-1\right) b\, d\tau \] where the integration goes from \(\tau=0\) to \(\tau=t\). Hence,
\[\log I(t) - \log I(0) = \int \left(R_{0}-1\right) b\, d\tau\] and therefore,
\[ I(t) = \exp\left\{ \int_{\tau=0}^{t} \left(R_{0}-1\right) b\, d\tau \right\}\, I(0)\] and assume the epidemic starts with only one infective so \(I(0)=1\). We deduce that the number of Infectives increases exponentially, decreases exponentially or stays constant, depending on the sign of \(R_{0}(t)-1\). In the event that \(R_{0}\) and \(b\) are independent of \(t\) or for \(t\approx 0\) we get,
\[ I(t) = \exp\left\{ (R_{0}-1) b t\right\}. \] In general, we have,
\[ R_{0}(t) = 1 + \frac{d I}{d R}\] which provides an easy way to estimate \(R_{0}(t)\) by replacing the infinitessimals with the daily observed increments,
\[ R_{0}(t) = 1 + \frac{\delta I}{\delta R}(t) \] This last equation also shows that \(R_{0}\) is independent of the size \(N\) of the population. It is obtained by adding \(1\) to the ratio of increments of Infective to Removed. No \(N\). Just increments of \(I\) and \(R\).
More precisely we would like to be able to prove the following,
Secondary infections are the infections produced by an infected individual. We can check the plausibility of the proposition by noticing that \(R_{0}\)s combine like averages combine. But, we do not have a probabilistic model yet, so what exactly does it mean to get the average at time \(t\)?
If we split \(N=N_{1}+N_{2}\) into two subpopulations with corresponding \(S_{1},I_{1},R_{1}\) and \(S_{2},I_{2},R_{2}\) then,
\[ R_{0} = \frac{N_{1}}{N_{1}+N_{2}}\, R_{0,1} + \frac{N_{2}}{N_{1}+N_{2}}\, R_{0,2} \] provided \(R_{1}/R_{2} = N_{1}/N_{2}\), i.e. the splitting is not done maliciously, for example collecting all the removed individuals into the second group and none in the first group. In other words, if the splitting produces two groups operating the same SIR epidemic we will expect \(R_{i}(t) = c(t) N_{i}\) with the same \(c(t)\) for \(i=1,2\). In this case, the above equation becomes,
\[ R_{0} = 1 + \frac{d I}{d R} = 1 + \frac{d R_{1}}{d R}\, \frac{d I_{1}}{d R_{1}} + \frac{d R_{2}}{d R}\, \frac{d I_{2}}{d R_{2}} = \frac{d R_{1}}{d R}\, R_{0,1} + \frac{d R_{2}}{d R}\, R_{0,2}\] where we have replaced \(1=dR_{1}/dR + dR_{2}/dR\). More over, for \(i=1,2\)
\[ \frac{d R_{i}}{dR} = \frac{N_{i} dc}{N_{1} dc + N_{2} dc} = \frac{N_{i}}{N_{1}+N_{2}}. \] Now \(R_{0}(t)\) is an average over the population that makes the infectives explode or collapse exponentially depending on the sign of \(R_{0}(t)-1\). This cannot be anything other than what is claimed. The average number of secondary infections. I am open to suggestions on how to tide this up. This will only make complete sense after assuming a probabilistic mechanism for the evolution of the pandemic process. For suppose we allow the possibility of \(N=\infty\) then the mean could become infinity itself and thus, the mean of the increments will become undefined.
The reproductive function \(R_{0}(t)\) is an invaluable overall summary of the evolution of the epidemic, that because is independent of the size of the population, can be used for making comparisons across scales, from small villages to whole continents. For approximating \(R_{0}(t)\) we need only daily estimates of the ratio: \(\delta I/\delta R\).
Exploratory estimation of \(R_{0}(t)\) for the Covid19 epidemic
source("https://omega0.xyz/continentalR0.R")-################### plots:
-#
-# plot 2 countries. Ver 1:
-# plot2R01('Chile','United States')
-# plot_country <- function(df,country,lead=5,dof=15)
-# R0 country:
-# plotR0 <- function(pais) plot_country(df,pais)
-#
-# R0 continent:
-# plotr0c <- function(df_continent,lead=5,dof=15)
-# the 6 continents:
-# plotR06c <- function(df=dfc)
-# Continents with variable lead and dof:
-# plot_R0sC <- function(lead=5,dof=15)
-# plot_mAUCc <- function(lead=5,dof=15) {
-# plot_median_AUCc(lead=5,dof=10)
-# mean AUC of continents:
-# plot_dfca <- function()
-# World:
-# plot_world <- function(lead=5,dof=15)
-# Population percents:
-# plot_pops <- function(continent='Africa') Suggestion to the reader:
Copy and paste the line of code above in an R session and follow along this document in a window next to your browser.
The list of some of the plots available includes the \(R_{0}(t)\) for the entire world,
plot_world()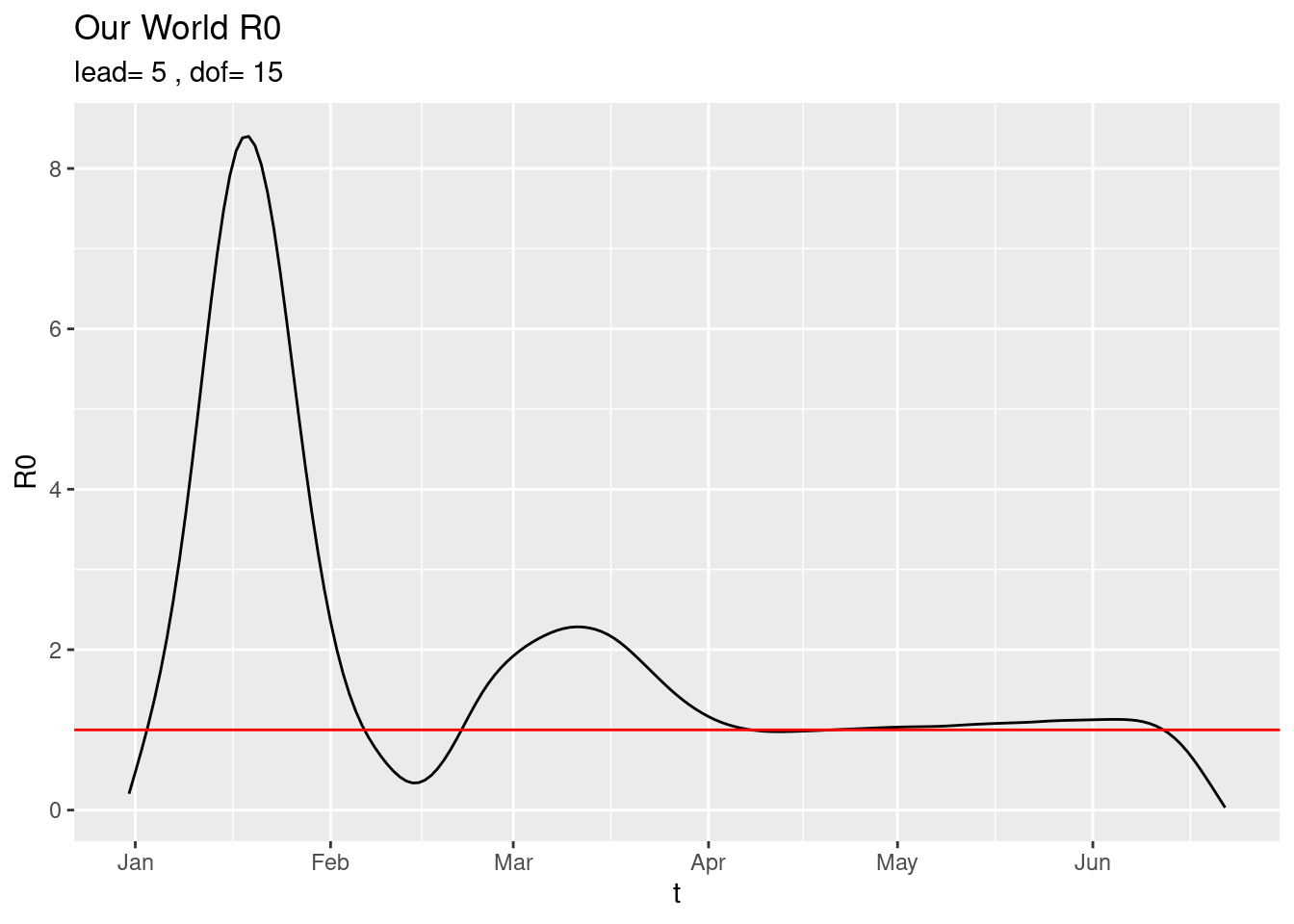
using current data. The estimation is done as follows:
The Infectives at day \(t\), \(I(t)\) is estimated as the new cases discovered day \(t\) plus all the new cases discovered a lead number of days into the future.
The Removed, \(R(t)\), are simply all the observed new cases upto day \(t\) plus all the observed new deaths upto day \(t\).
\[ R_{0}(t) = 1 + \frac{\delta I}{\delta R} (t)\]
\[ 1 + \cdot /0 = 1\]
The smoothing spline with dof degrees of freedom of the raw estimator is the curve shown above.
For example a drastic smoother is just the overall trend (line) obtained with,
plot_world(dof=2)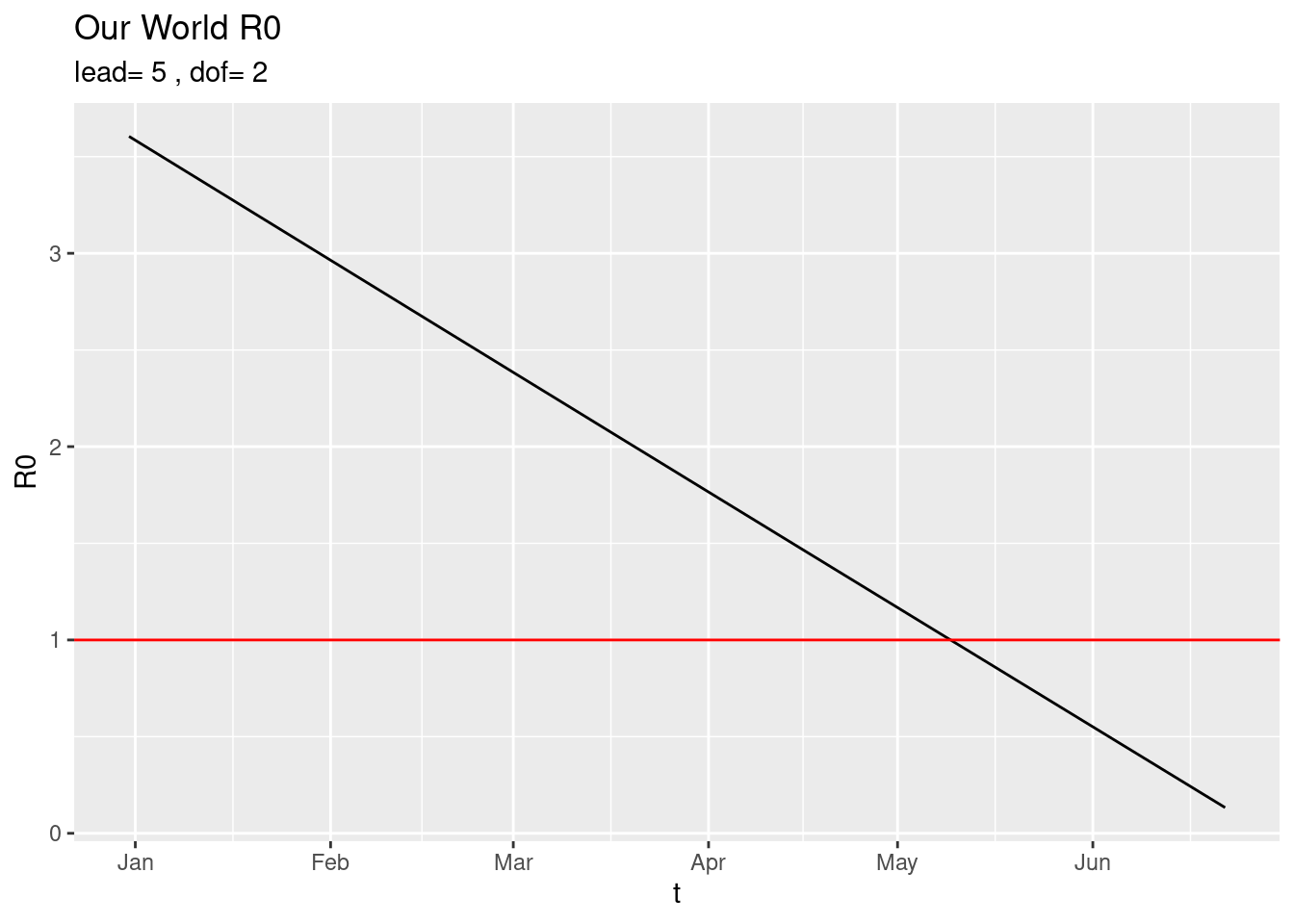
and with very little smoothing,
plot_world(dof=80)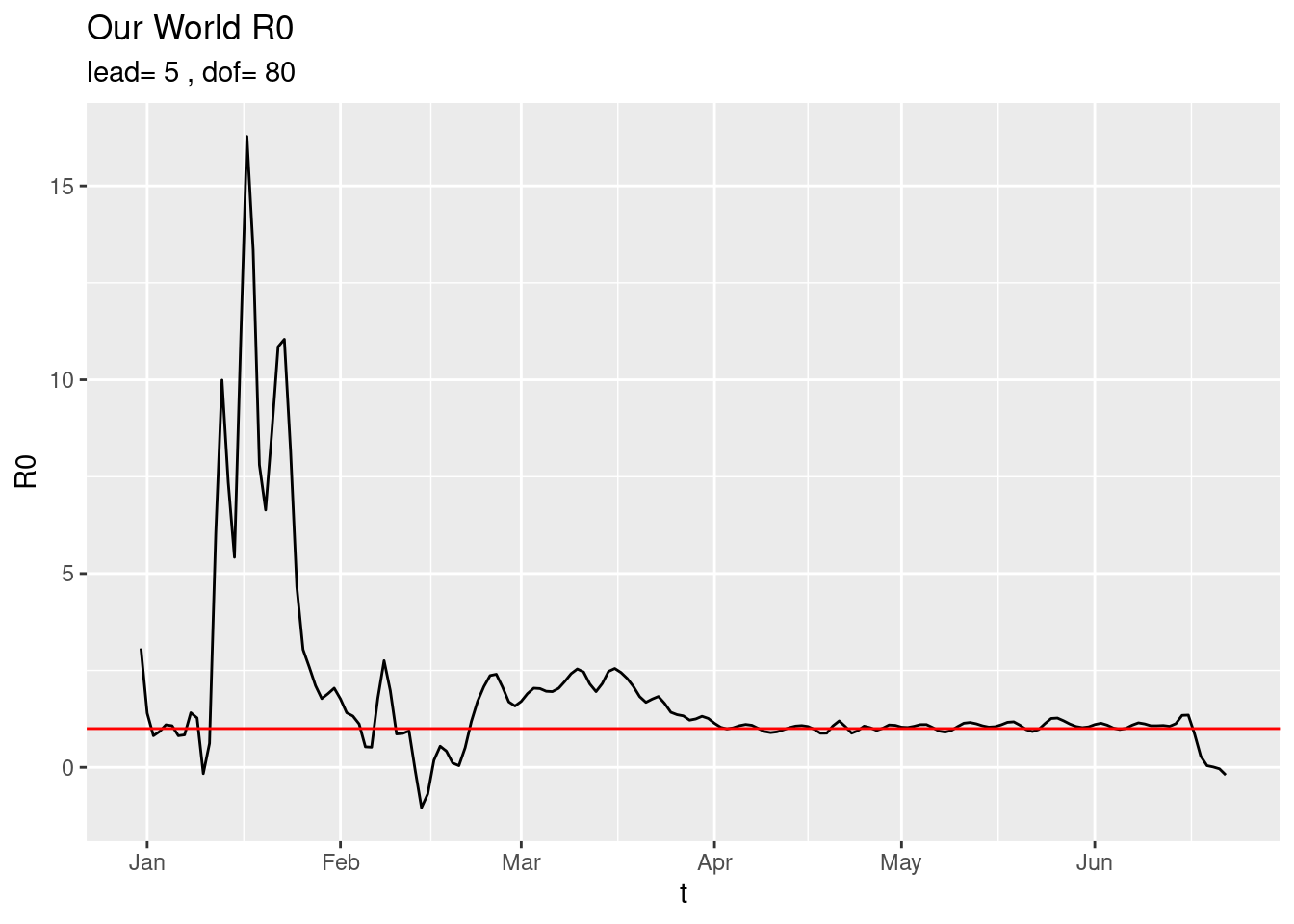
The current picture of the six continents is,
plot_R0sC()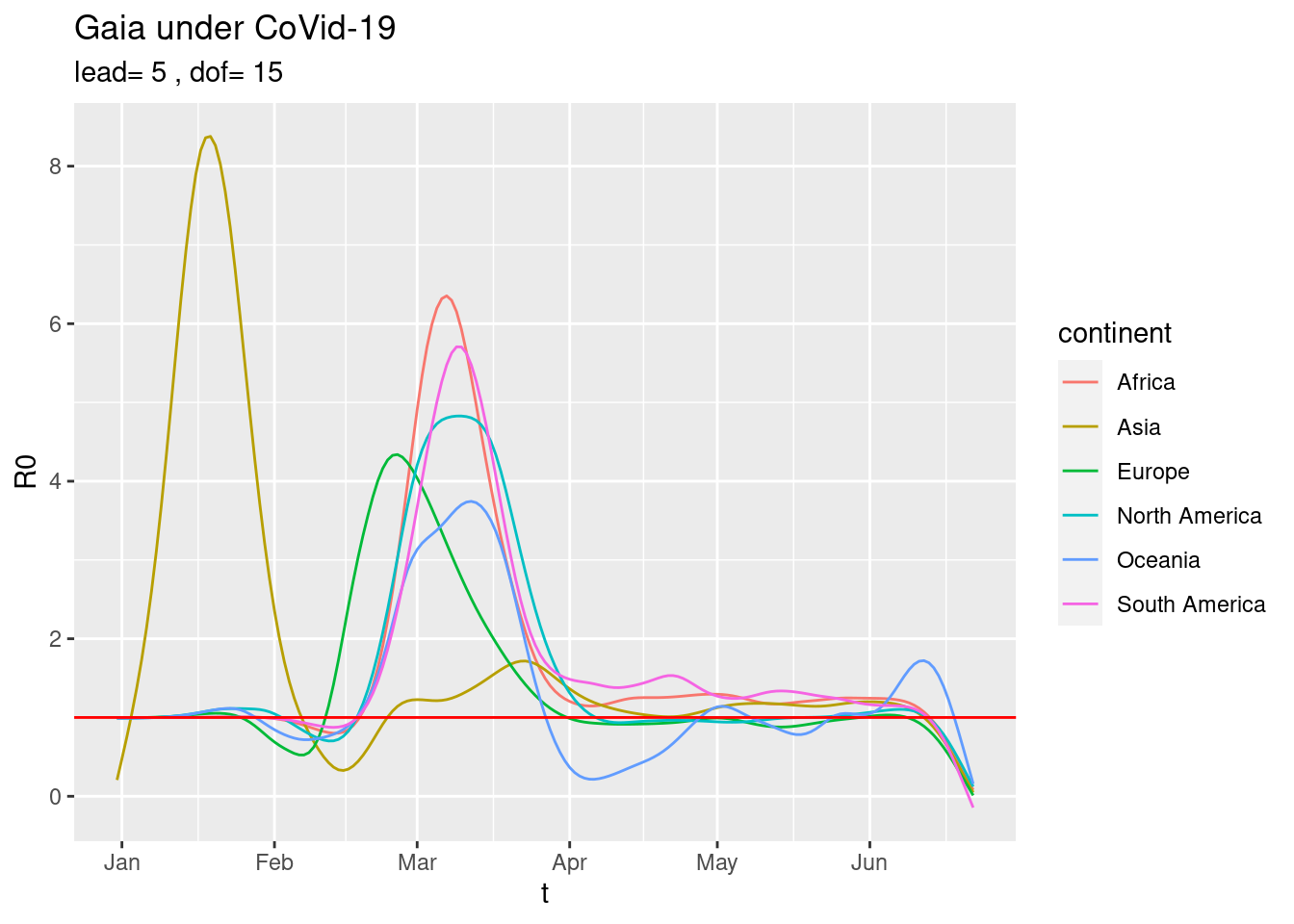
or just the current trends,
plot_R0sC(dof=2)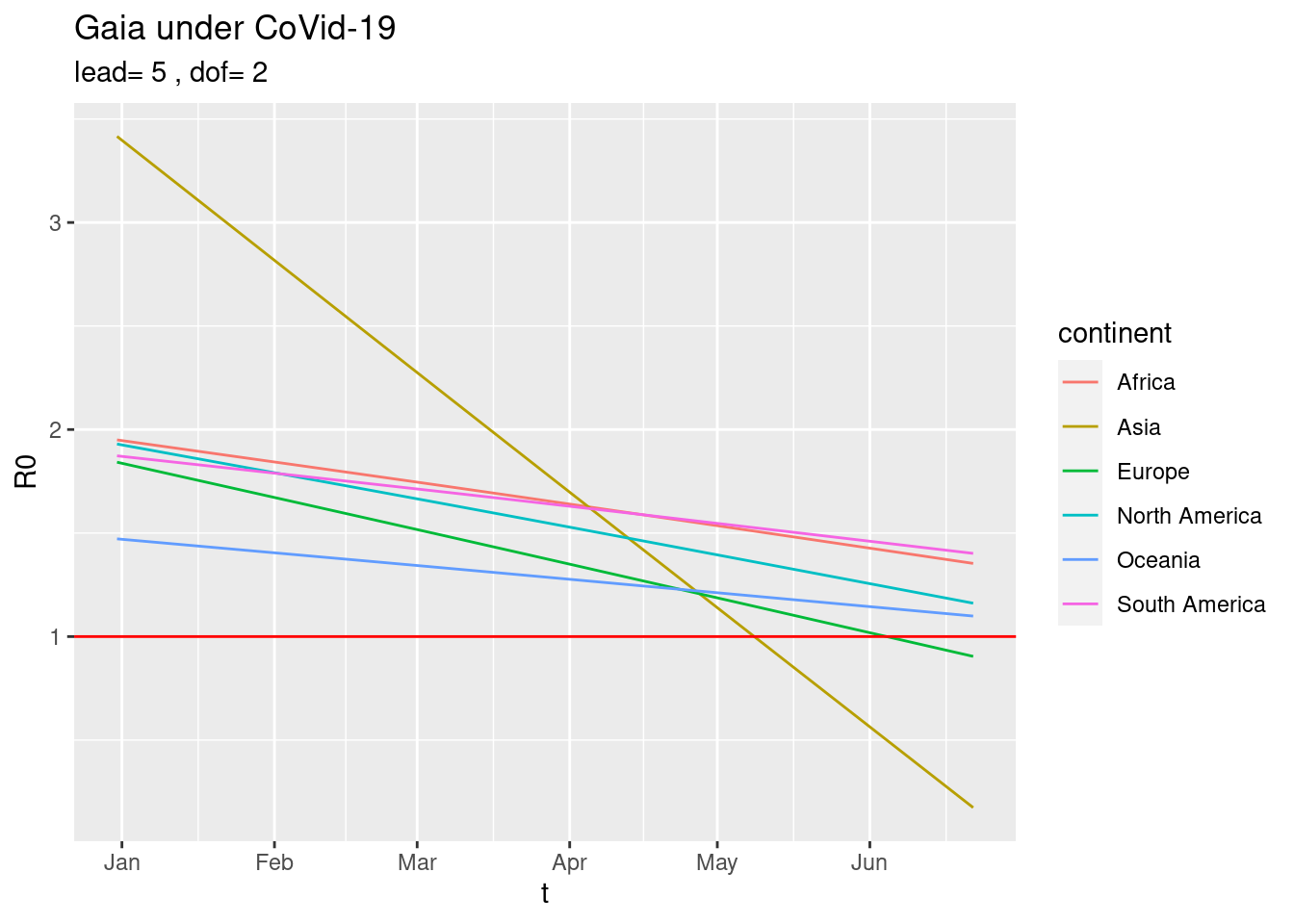
Compare two countries
plot2R01('Spain','Italy')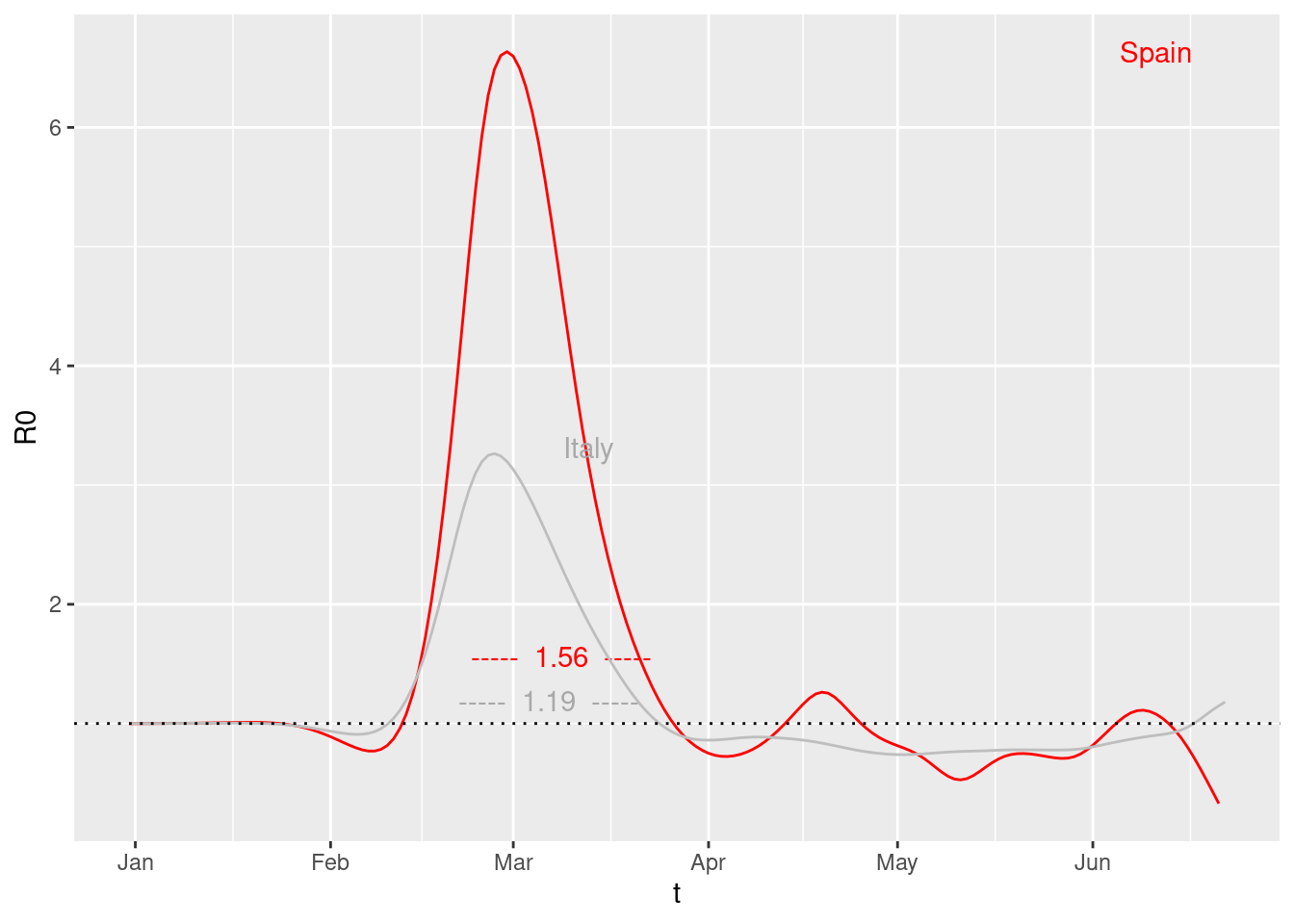
OMG! look at Italy.
Overall sizes for the \(R_{0}\) of the six continents,
plot_median_AUCc()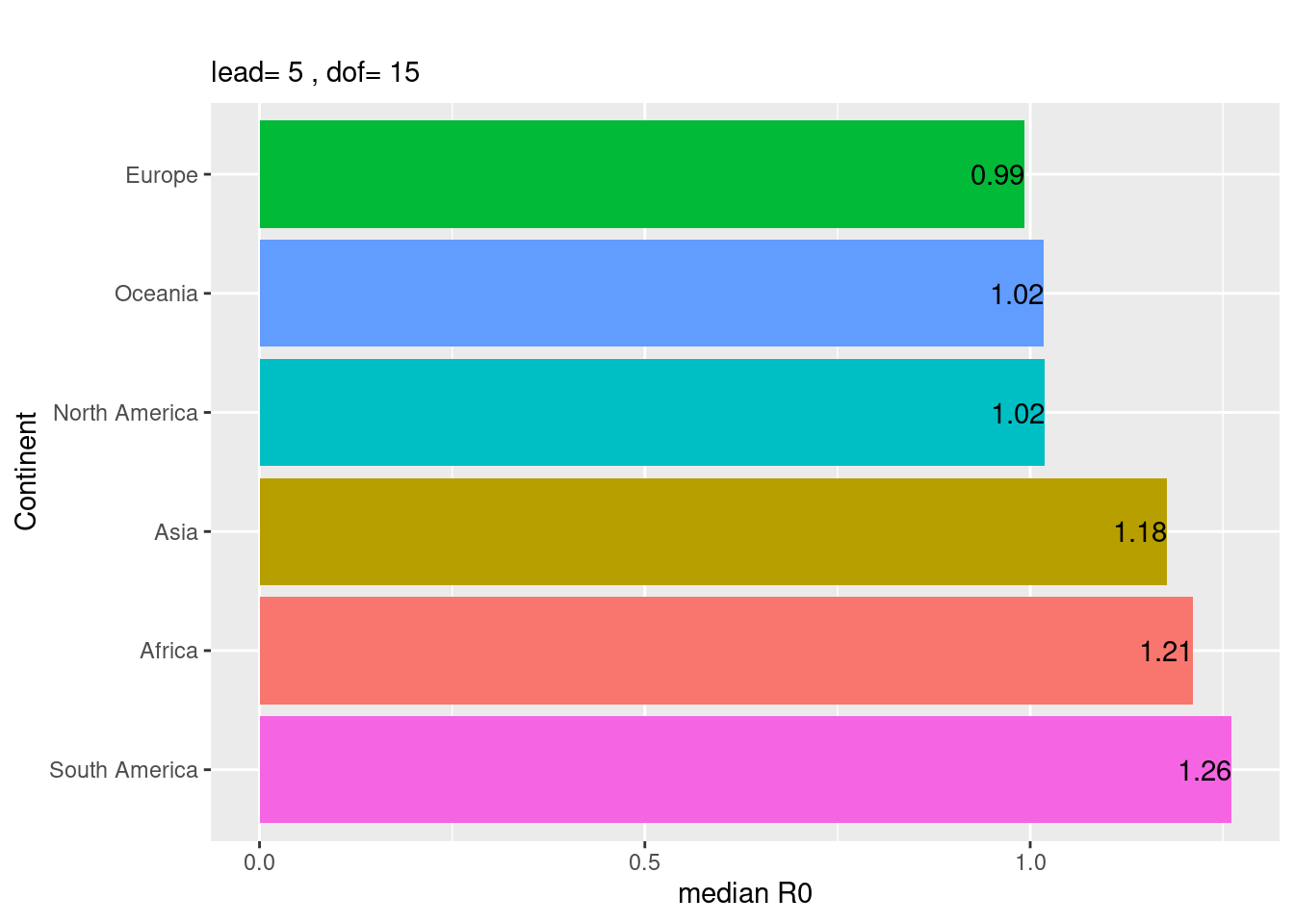
Names of countries
countries## [1] "Afghanistan" "Albania"
## [3] "Algeria" "Andorra"
## [5] "Angola" "Anguilla"
## [7] "Antigua and Barbuda" "Argentina"
## [9] "Armenia" "Aruba"
## [11] "Australia" "Austria"
## [13] "Azerbaijan" "Bahamas"
## [15] "Bahrain" "Bangladesh"
## [17] "Barbados" "Belarus"
## [19] "Belgium" "Belize"
## [21] "Benin" "Bermuda"
## [23] "Bhutan" "Bolivia"
## [25] "Bonaire Sint Eustatius and Saba" "Bosnia and Herzegovina"
## [27] "Botswana" "Brazil"
## [29] "British Virgin Islands" "Brunei"
## [31] "Bulgaria" "Burkina Faso"
## [33] "Burundi" "Cambodia"
## [35] "Cameroon" "Canada"
## [37] "Cape Verde" "Cayman Islands"
## [39] "Central African Republic" "Chad"
## [41] "Chile" "China"
## [43] "Colombia" "Comoros"
## [45] "Congo" "Costa Rica"
## [47] "Cote d'Ivoire" "Croatia"
## [49] "Cuba" "Curacao"
## [51] "Cyprus" "Czech Republic"
## [53] "Democratic Republic of Congo" "Denmark"
## [55] "Djibouti" "Dominica"
## [57] "Dominican Republic" "Ecuador"
## [59] "Egypt" "El Salvador"
## [61] "Equatorial Guinea" "Eritrea"
## [63] "Estonia" "Ethiopia"
## [65] "Faeroe Islands" "Falkland Islands"
## [67] "Fiji" "Finland"
## [69] "France" "French Polynesia"
## [71] "Gabon" "Gambia"
## [73] "Georgia" "Germany"
## [75] "Ghana" "Gibraltar"
## [77] "Greece" "Greenland"
## [79] "Grenada" "Guam"
## [81] "Guatemala" "Guernsey"
## [83] "Guinea" "Guinea-Bissau"
## [85] "Guyana" "Haiti"
## [87] "Honduras" "Hong Kong"
## [89] "Hungary" "Iceland"
## [91] "India" "Indonesia"
## [93] "Iran" "Iraq"
## [95] "Ireland" "Isle of Man"
## [97] "Israel" "Italy"
## [99] "Jamaica" "Japan"
## [101] "Jersey" "Jordan"
## [103] "Kazakhstan" "Kenya"
## [105] "Kosovo" "Kuwait"
## [107] "Kyrgyzstan" "Laos"
## [109] "Latvia" "Lebanon"
## [111] "Lesotho" "Liberia"
## [113] "Libya" "Liechtenstein"
## [115] "Lithuania" "Luxembourg"
## [117] "Macedonia" "Madagascar"
## [119] "Malawi" "Malaysia"
## [121] "Maldives" "Mali"
## [123] "Malta" "Mauritania"
## [125] "Mauritius" "Mexico"
## [127] "Moldova" "Monaco"
## [129] "Mongolia" "Montenegro"
## [131] "Montserrat" "Morocco"
## [133] "Mozambique" "Myanmar"
## [135] "Namibia" "Nepal"
## [137] "Netherlands" "New Caledonia"
## [139] "New Zealand" "Nicaragua"
## [141] "Niger" "Nigeria"
## [143] "Northern Mariana Islands" "Norway"
## [145] "Oman" "Pakistan"
## [147] "Palestine" "Panama"
## [149] "Papua New Guinea" "Paraguay"
## [151] "Peru" "Philippines"
## [153] "Poland" "Portugal"
## [155] "Puerto Rico" "Qatar"
## [157] "Romania" "Russia"
## [159] "Rwanda" "Saint Kitts and Nevis"
## [161] "Saint Lucia" "Saint Vincent and the Grenadines"
## [163] "San Marino" "Sao Tome and Principe"
## [165] "Saudi Arabia" "Senegal"
## [167] "Serbia" "Seychelles"
## [169] "Sierra Leone" "Singapore"
## [171] "Sint Maarten (Dutch part)" "Slovakia"
## [173] "Slovenia" "Somalia"
## [175] "South Africa" "South Korea"
## [177] "South Sudan" "Spain"
## [179] "Sri Lanka" "Sudan"
## [181] "Suriname" "Swaziland"
## [183] "Sweden" "Switzerland"
## [185] "Syria" "Taiwan"
## [187] "Tajikistan" "Tanzania"
## [189] "Thailand" "Timor"
## [191] "Togo" "Trinidad and Tobago"
## [193] "Tunisia" "Turkey"
## [195] "Turks and Caicos Islands" "Uganda"
## [197] "Ukraine" "United Arab Emirates"
## [199] "United Kingdom" "United States"
## [201] "United States Virgin Islands" "Uruguay"
## [203] "Uzbekistan" "Vatican"
## [205] "Venezuela" "Vietnam"
## [207] "Western Sahara" "Yemen"
## [209] "Zambia" "Zimbabwe"
## [211] "World" "International"