|
|
Problem1:
| Let |
> u := [2,1]: v:= [-3,4]:
|
Sketch the vector,
|
|
|
Solution1:
| We can write a function for finding the vector for the different values of c. |
> mix := c -> evalm(c*u+(1-c)*v);
mix := c -> evalm(c u + (1 - c) v)
| The four vectors are, |
> m0:=mix(0); m1:= mix(1/4); m2:= mix(3/4); m3 := mix(1);
m0 := [-3, 4]
m1 := [-7/4, 13/4]
m2 := [3/4, 7/4]
m3 := [2, 1]
These vectors are along the segment from v to u.
m1 is 1/4 of the way along and m2 is 3/4 of the way along u-v
(look at the picture).
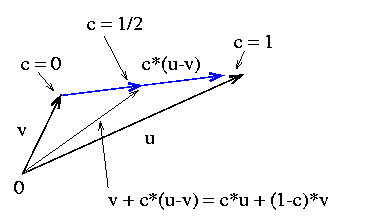 |
|
This shows that if the initial point fo cu+(1-c)v for
0 |