Problem:Find the equation of the plane determined by the lines L1 and L2 where, |
> L1 := {(x+3)/3 = y/(-2), y/(-2) = (z-7)/6}; L2 := {(x+6)/1 = (y+5)/(-3),(y+5)/(-3) =(z-1)/2};
L1 := {1/3 x + 1 = - 1/2 y, - 1/2 y = 1/6 z - 7/6}
L2 := {x + 6 = - 1/3 y - 5/3, - 1/3 y - 5/3 = 1/2 z - 1/2}
| The intersection point is, |
> solve( L1 union L2,{x,y,z});
{y = 4, z = -5, x = -9}
| The normal to the plane is perpendicular to the direction vectors of L1 and L2, |
> n := crossprod([3,-2,6],[1,-3,-3]);
n := [ 24, 15, -7 ]
| and the equation of the plane is, |
> Plane := innerprod(n,[x+9,y-4,z+5]) = 0;
Plane := 24 x + 121 + 15 y - 7 z = 0
| and sort the terms with, |
> Plane := sort(Plane,[x,y,z]);
Plane := 24 x + 15 y - 7 z + 121 = 0
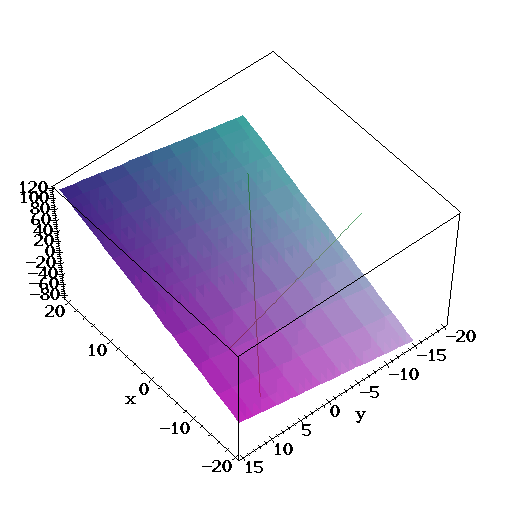
| Let's plot it all! We start with L1 and L2, |
> with(plots):
> picL1 := spacecurve(evalm([-3,0,7]+t*[3,-2,6]),t=-5..5):
> picL2 := spacecurve(evalm([-6,-5,1]+t*[1,-3,-3]),t=-5..5):
> picPlane := plot3d( solve(Plane,z), x=-20..20, y=-15..15,grid=[5,5]):
> display3d({picL1,picL2,picPlane});