PROBLEM |
> z := x^2 - sin(x*y);
2
z := x - sin(x y)
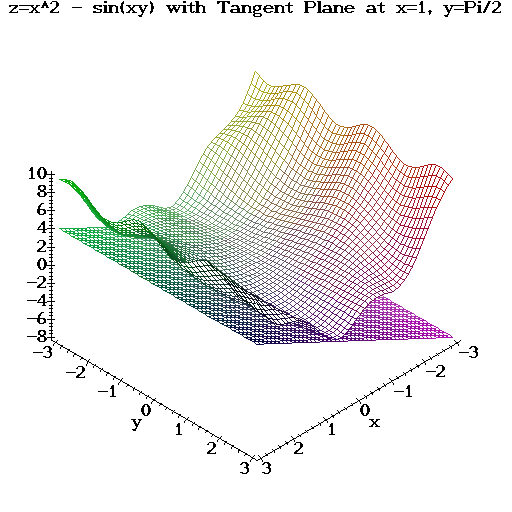
Find the equation of the tangent plane at x=1, and y=Pi/2. Display a picture of this surface together with
the tangent plane.
Solution |
> f := unapply(z,x,y): dx := x-1: dy := y-Pi/2:
> fx := subs({x=1,y=Pi/2}, diff(z,x)):
> fy := subs({x=1,y=Pi/2}, diff(z,y)):
> Z := f(1,Pi/2) + fx*dx + fy*dy;
Z := 2 x - 2
> plot3d({z,Z}, x=-3..3, y=-3..3, grid=[50,50], axes=framed, title=`z=x^2 - sin(xy) with Tangent Plane at x=1, y=Pi/2`);

Problem2:Write a maple procedure for computing the equation of a general tangent plane at an arbitrary point. The procedure should receive as input: an expression "z" in x and y and the point (a,b). Call the procedure, Tplane.Solution2: |
> Tplane := proc(z,a,b) local fx,fy,dx,dy,z0,Z;
> z0 := subs({x=a,y=b},z);
> dx := x-a;
> dy := y-b;
> fx := subs({x=a,y=b},diff(z,x));
> fy := subs({x=a,y=b},diff(z,y));
> Z := simplify( z0 + fx*dx + fy*dy);
> Z := collect(Z,[x,y]);
> Z := sort(Z,[x,y]);
> end;
Tplane := proc(z,a,b)
local fx,fy,dx,dy,z0,Z;
z0 := subs({x = a,y = b},z);
dx := x-a;
dy := y-b;
fx := subs({x = a,y = b},diff(z,x));
fy := subs({x = a,y = b},diff(z,y));
Z := simplify(z0+fx*dx+fy*dy);
Z := collect(Z,[x,y]);
Z := sort(Z,[x,y])
end
| Let's test it, |
> Z1 := Tplane(z,1,Pi/2);
Z1 := 2 x - 2
|
That was quick! Another one: The equation of the tangent plane to the unit sphere centered at the origin at the point x=1/2,y=1/2.
|
> Z := Tplane(sqrt(1-x^2-y^2),1/2,1/2);
1/2 1/2 1/2
Z := - 1/2 2 x - 1/2 2 y + 2
|
The last one: Find the equation of the tangent plane to the surface, We first have to to solve for z, |
> solve(x*y^2*z^3 = 12,z);
1/3 / 1 \1/3 1/3 / 1 \1/3 1/2 1/3 / 1 \1/3
12 |----| , - 1/2 12 |----| + 1/2 I 3 12 |----| ,
| 2| | 2| | 2|
\x y / \x y / \x y /
1/3 / 1 \1/3 1/2 1/3 / 1 \1/3
- 1/2 12 |----| - 1/2 I 3 12 |----|
| 2| | 2|
\x y / \x y /
|
OOOOPPPPSSS! Don't panic. Notice that maple (as usual) tries to be too smart and consider ALL the possible solutions. There are three solutions separated by commas. Can you see them? We only need the real (first) solution. The second and third are complex (Do you see the I?). Let's grab the first one with, |
> z := solve(x*y^2*z^3 = 12,z)[1];
1/3 / 1 \1/3
z := 12 |----|
| 2|
\x y /
| Now the tangent plane, |
> Z3 := Tplane(z,3,2);
Z3 := - 1/9 x - 1/3 y + 2
| How about a picture? |
> plot3d({z,Z3},x=0.1..5,y=0.5..5,grid=[50,50]);