Vectors

1. Scalars- Magnitude Only. e.g. Mass, Length and Time.
2. Vectors- Magnitude and Direction. e.g. Velocity and Force.
3. Tensors- Not covered here.

The simplest way to differentiate vectors from scalars is to take Speed vs. Velocity.

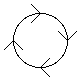In the path shown above, assume that the particle has a fixed speed. While it's speed does not change, it does have an acceleration, as the direction changes constanly.

• Free Vectors vs. Bound Vectors

  In this course we will be dealing with free vectors. Free vectors are deemed to be equal if they have the same magnitude and direction, regardless of their location. The same does not hold true for bound vectors.
  • Free Vectors

    

  • Bound Vectors

    

• Unit Vectors

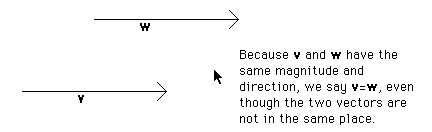
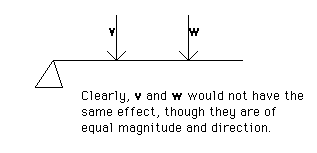
  Def: A unit vector is a vector of length (magnitude) one.

  The 2-D space with which we are very familiar has two particular unit vectors reffered to as a "Basis." They are the i and j vectors. Because they are a Basis every vector can be written in terms of these two vectors. For example v = 3i + 2j. Thus, one can determine the components of v. It is important; however, to differentiate between the scalar and vector components.

  Scalar Components: 3,2 Vector Components: 3i, 2j

• Laws of Addition

  There are two ways to add vectors, geometrically and algebraically.

  • Geometric Addition

    

  • Algebraic Addition

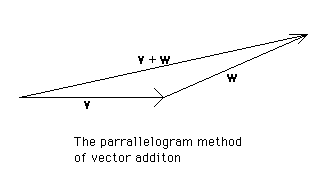
    v = 3i - 2j, w = i + j

    v + w = 4i - j

• Magnitude

  The Magnitude of a vector is it's length, defined in 2-D as below.

  

• Direction

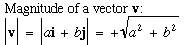
  Def: The direction of v is a unit vector parallel to v

  

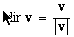
  For example:

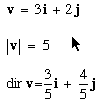
  But what does this mean? We usually think of direction in terms of angles, not components of vectors. This brings us to slope.

• Slope

  

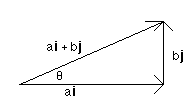
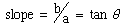
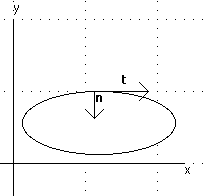
  This can be used to find unit tangents and normals to curves defined in the x-y plane. Any curve will have two unit tangents and two unit normals at any point, so it is necessary to differentiate betweent the clockwise and counterclockwise tangents and the in and out unit normals. The example below shows an inward unit normal and a clockwise unit tangent.

  

  In order to find these tangents, it is necessary to "marry" calculus and slope. Since the derivitive, dy/dx, is equal to the slope, b/a, you can find the unit tangent vector simply by setting these two quantities equal to each other. Namely:

  dy/dx = b/a