| Consider a vector curve f. The derivative of f at t points in the direction of the tangent line of the curve at f(t). For example, consider the following curve: |
> f := t -> t^2*i + (1-t)^2*j + t^3*k;
2 2 3
f := t -> t i + (1 - t) j + t k
| The equation of the tangent line at t=s is given by, |
> Dfs := D(f)(s); L := t -> f(s) + t*Dfs;
2
Dfs := 2 s i - 2 (1 - s) j + 3 s k
L := t -> f(s) + t Dfs
| A picture of the curve together with the tangent lines at, t=0, and t=1 is given by, |
> with(plots):
> C := spacecurve(evalm(f(t)),t=-2..2): s:=0;
s := 0
> L0:= spacecurve(evalm(L(t)), t=-2..2,color=GREEN): s:=1;
s := 1
> L1 := spacecurve(evalm(L(t)),t=-2..2,color=GREEN): 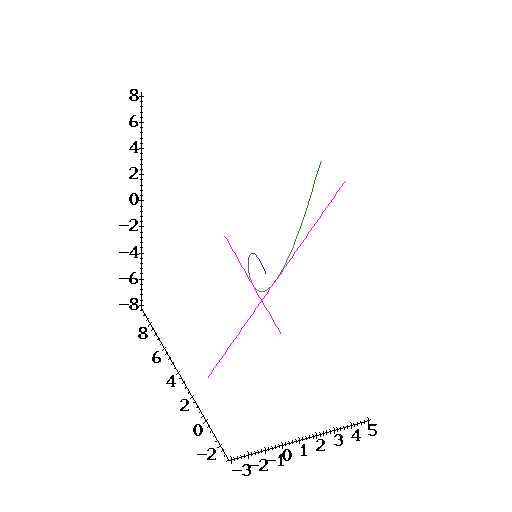
len := proc(u) sqrt(innerprod(evalm(u),evalm(u))) end
| The unit tangent vector to a curve at t=s is denoted by T(s). We have, |
> T := s -> D(f)(s)/len(D(f)(s));
D(f)(s)
T := s -> ------------
len(D(f)(s))
| As we can see the derivative of T(s) is always orthogonal to T(s) itself,since T(s) has constant length of 1. The principal unit normal is defined by, |
> Ns := collect(diff(T(s),s)/len(diff(T(s),s)),[i,j,k]);
/ 3 \
| 2 (16 s - 8 + 36 s ) s| 1/2
|----- - --------------------| 2 i
| 1/2 3/2 |
\%1 %1 /
Ns := 1/4 -------------------------------------
/ 4 3 2 \1/2
|9 s - 18 s + 18 s + 2|
|------------------------|
| 2 |
\ %1 /
/ 3 \
| 2 (16 s - 8 + 36 s ) (- 2 + 2 s)| 1/2
|----- - 1/2 ------------------------------| 2 j
| 1/2 3/2 |
\%1 %1 /
+ 1/4 ---------------------------------------------------
/ 4 3 2 \1/2
|9 s - 18 s + 18 s + 2|
|------------------------|
| 2 |
\ %1 /
/ 3 2\
| s (16 s - 8 + 36 s ) s | 1/2
|6 ----- - 3/2 ---------------------| 2 k
| 1/2 3/2 |
\ %1 %1 /
+ 1/4 --------------------------------------------
/ 4 3 2 \1/2
|9 s - 18 s + 18 s + 2|
|------------------------|
| 2 |
\ %1 /
2 4
%1 := 8 s + 4 - 8 s + 9 s
| This is just the derivative of T at s over its length. For example at s=0 and s=1 we have, |
> N := unapply(Ns,s): T(0), simplify(N(0));
- j, i
| Clearly perpendicular to each other. And, |
> T(1), simplify(N(1));
1/2
1/13 (2 i + 3 k) 13 ,
1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2
- 9/286 13 2 11 i + 1/22 13 2 11 j + 3/143 13 2 11 k
| Not so clear this time , but, |
> innerprod(T(1),N(1));
0
| In fact: |
> innerprod(T(s),N(s));
0