| A vector function is a function that produces a vector. The typical example is the trajectory of a particle in space. At each time "t" the particle has position vector "r(t)". In a given coordinate system we can write the componets of "r(t)" in terms of the basis vectors i,j and k. Here is an example: |
> i := vector([1,0,0]): j:=vector([0,1,0]): k:=vector([0,0,1]):
> r := t -> cos(t)*i + sin(t)*j + t*k;
r := t -> cos(t) i + sin(t) j + t k
| Hence, the positions of the particle at times t=0, t=Pi/2 and t=Pi are given by the vectors: |
> r(0); r(Pi/2); r(Pi);
i
j + 1/2 Pi k
- i + Pi k
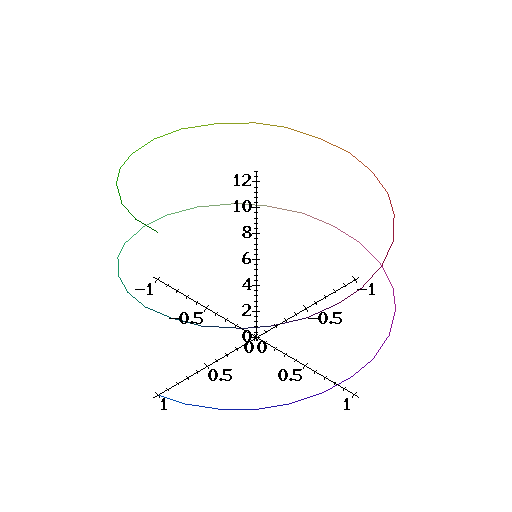
| Here is a picture of this curve |
> with(plots):
> spacecurve(evalm(r(t)), t=0..4*Pi, color=YELOW,axes=NORMAL);
LimitsThe fundamental concept of Calculus is the concept of "limit". Once you know how to compute limits, the definitions of "continuity", "derivative", and "integral" will follow easily. If you revise your Calc I notes you will soon discover that the definition of limit depends only on the concept of distance between two points. It then follows that if you know how to compute the distance between two points then you also know how to compute the limit of a function that takes values (or that it is defined) in that space of points.
The definition of limit, in words, is:
The equivalent epsilon (e), delta (d), definition is: It suffices to replace: |z| with the magnitude of the vector z (i.e. sqrt(innerprod(z,z))) to obtain the general definition of "limit" in any number of dimensions. In particular it folows (prove it) that if the function f takes a real number t into an n-dimensional vector y = (y1,y2,...,yn) then each of the coordinates of y are real-valued functions of the real variable t or, and
Limit f(t) = z = (z1,z2,...,zn)
t -> t0
if and only if,
Limit f1(t) = z1
t -> t0
Limit f2(t) = z2
t -> t0
.
.
.
Limit fn(t) = zn
t -> t0
So in this case there is nothing new to be learned. To compute the
limit of a vector-valued function of a single variable t, all we need to
do is to compute several limits of real-valued functions of the
variable t. In this case the difference between Calc I and Calc III
is that in Calc I you need to do it once but in Calc III you need
to do it 3 times! So,... Just do it!
By the way the (meta)-equation: Let's work out an example of limits with Maple. Let |
> f := t -> expand(r(t)/t): `f(t)` = f(t);
cos(t) i sin(t) j
f(t) = -------- + -------- + k
t t
| and to compute the limit of f(t) when t approaches 0 all we (well in this case, Maple) need to do is to compute the limits when t goes to 0 for each of the three coordinate functions of f. |
> Limit(`f(t)`,t=t0) = expand(limit(f(t),t=t0));
cos(t0) i sin(t0) j
Limit f(t) = --------- + --------- + k
t -> t0 t0 t0
| But when t0 = 0, |
> Limit(`f(t)`,t=0) = limit(f(t),t=0);
Limit f(t) = undefined
t -> 0
| Which is the correct answer since the limit of the first coordinate function does not exist at 0. Here are other limits, |
> Limit(`f(t)`,t=Pi/4) = expand(limit(f(t),t=Pi/4));
1/2 1/2
2 i 2 j
Limit f(t) = 2 ------ + 2 ------ + k
t -> (1/4 Pi) Pi Pi
Limit f(t) = .896 i + .896 j + k
t -> (1/4 Pi)
| One more limit, now at t=135 degrees, |
> Limit(`f(t)`,t=3*Pi/4) = expand(simplify(limit(f(t),t=3*Pi/4)));
1/2 1/2
2 i 2 j
Limit f(t) = - 2/3 ------ + 2/3 ------ + k
t -> (3/4 Pi) Pi Pi
|
Easy ha? Do you remember the old tune (that you used to sing in Calc I)? it goes....
Look at this, |
> Limit(a*`f(t)` + b*`r(t)`,t=s) = limit(a*f(t)+b*r(t),t=s);
(cos(s) i + sin(s) j + k s) (a + b s)
Limit a f(t) + b r(t) = -------------------------------------
t -> s s
so what do you say? Does it sound like the old tune?
ContinuityWe say that a vector valued function r is continuous at t=a if,
Limit r(t) = r(a)
t -> a
Thus, the helix is continuous at t=0 but the function f defined above is not.
|