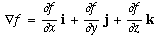
In Lecture 3 we finished up the topic of line integrals. In this lecture we move on to the subject of the Gradient function, and how it relates to surfaces in space.

1. You can define a function f(x,y,z) and require that it always have the same constant value; f(x,y,z)=C.
   For Example, a sphere would have f(x,y,z)=x^2 + y^2 + z^2, and C=R^2, where R is the radius of the sphere.
2. You can also set z to be a function of x and y; z=g(x,y). For the same sphere as above, this would give you:
   z=+sqrt(R^2-x^2 - y^2) and z=-sqrt(R^2-x^2 - y^2)
   

The Gradient

The gradient of a function is a Vector defined as:

grad f =

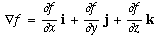
1. If u is a unit vector, the derivative of a function f(x,y,z) in the u direction is f (dot) u. The derivative of f in the u direction is defined to be the limit below:
   v=xi+yj+zk,
   and u is a unit vector.
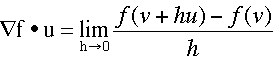
2. The direction of f(x,y,z) is the direction of "steepest ascent" of the surface.
   This can be seen by looking back at the first usage of the gradient. If you attempt to maximize f (dot) u, you can see that this is the case when f is in the same direction as u. Thus, the direction of most severe change in f is the direction of f.

3. Given z=g(x,y) representing a surface (hill),
   
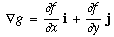
   g will point in the direction in the (x,y) plane you would walk to go up the steepest part of the hill, and ||g|| would be the slope of the hill.

   Level Curves: Level Curves are curves in the x-y plane that trace out g(x,y)=C, where C is a constant. That is, curves which yield a constant height on the hill created by z=g(x,y).

   g points perpendicular to the level curves.
   This can be proven by thinking about the first use of gradients again. g (dot) u is the derivitive in the u direction. g (dot) T, a tangent to a level curve, is the change of g when one moves in the T direction. Since T is along a line of g(x,y) = A constant, there is no change. So g (dot) T = 0. Thus, g must be perpendicular to T, and therefore to the level curve.

4. Let f(x,y,z) = C define a surface.
   f is perpindicular to the surface.
   The proof of this is also fairly simple.
   Take C, an arbitrary path along the surface, and T, the unit tangent to that path. The derivative of f along C is 0, since f(x,y,z) = a constant on the surface, and thus does not change as you move along the surface. So, f (dot) T = 0.
   Since C is an arbitrary path, this implies that f is perpendicular to the surface.
   Thus the normal to a surface defined by f(x,y,z) = C is f / ||f||

---

An Example:
Given the paraboloid z= g(x,y) = x^2 + y^2 - C or f(x,y,z) = x^2 - y^2 - z = C
Find f, g, observe the relationship between them, and find the derivitive of f in the x direction.

g = 2xi + 2yj = 2(xi + yj)
f = 2xi + 2yj - k

Note that g is the projection of f onto the x-y plane.

To find the derivative of f in the x (i) direction:

f (dot) i = 2x

---

Lecture written by Lawrence C. Weintraub on Sunday, September 17, 1995
Edited by Aric Shafran on Sunday, September 17, 1995
Make a comment using the feedback page
or by sending e-mail to: <mb49@cornell.edu> or <lcw5@cornell.edu> or <aps6@cornell.edu>

---