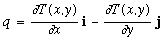
In Lecture 1 we learned how to evaluate a line integral, and did a short, fairly simple example. In this lecture we discuss an application of the line integral - computing the work done to move an object through a Force field.

• Vector Field - A vector valued quantity defined over some space.

For example - The Flow Field for a Fluid, which gives the velocity of the fluid at every point in a given space.
Another Example would be the heat flow vector:

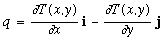
In General, a Vector Field F, will be defined by

Line Integrals Involving Vector Fields

The Work Integral

Given a path and a force field:

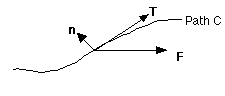
F = Vector Force Field Acting on Particle
T = Unit Tangent Vector
n = Unit Normal Vector

The work increment in moving a differential length ds along the path is
dW = F (dot) T ds
= Force dotted with direction, times distance.

The total work done by force on a particle as it moves along a path C is:

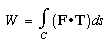
This is a line integral, with f(x,y,z) = F (dot) T

So, we just define C: r(t) = x(t)i + y(t)j + z(t)k a<=t<=b
ds = ||v(t)|| dt
T = v(t)/||v(t)||
v(t) = dr/dt

• Work along C1: F(x,y,z) = t*ti + tj - t*tk
  v = i + j + k
  

• Work along C2
  F(x,y,z) = t^3i + t^2j - t^5k
  v = i + 2tj + 3t^2k
  

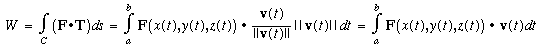
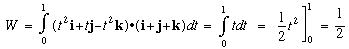
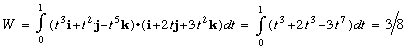
  Note that work here was different depending on the path chosen for the particle.

Summary

1. Parametrize the path C.
2. Find v(t)
3. Subsitute x(t) for x, y(t) for y, etc. into F(x,y,t) to make it a function of t only.(t)
4. Do the Integral from a->b of F( x(t), y(t), z(t) ) (dot) v(t) dt