|
|
Cartesian and Polar Rectangles
|
Recall that a system of coordinates on the eucliean plane is only
an artifact that allows us to assign a numeric label to all the points
on the plane. The quantities that have intrinsic geometric meaning
should be independent of the arbitrary labeling (coordinate) system
used. In particular integrals, that as we know represent areas and volumes,
must be invariant under changes of coordinate systems. After all the
ammount of water that we can put in a container
(the volume of the container measured by an integral) is the same wether
we label the points with cartesian or any other system of coordinates.
We show here how the expression of an integral changes when we use one or other system of coordinates but the value of the integral always stays put. The definition of an integral is always the same: partition the domain of integration into n little pieces, pick a point inside each piece, compute the size of each piece and the value of the function at the chosen point inside each piece and finally produce the number sum f(point)*size(piece). The sequence of these numbers when n increases (and the size of each piece decreases to 0) converges to what we call the integral of f over the given domain. Notice that each of the steps used to define the concept of integral have intrinsic geometric meaning and therefore the definition is in fact coordinate free. It is a theorem (shown in more advance calculus) that when the integral exists, it does not depend on the sequence of partitions used to approximate it. That is, as long as the partition gets finner and finner the Riemann sums will approach the same limit no matter what shape the pieces are and no matter what point is chosen inside each piece.
When computing integrals, a change in the coordinate system of the space
can be thought as a change in the way we partition the domain of
integration. Each system of coordinates comes equipped with a standard
notion of piece. To fix the ideas let us consider the euclidean
plane with cartesian (x,y) and polar (r,t) coordinates (see figure).
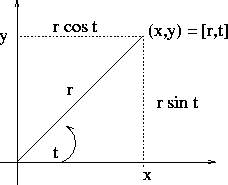 We define a rectangle, in a system of coordinates (u,v), as the region: |
> #
R := {(u,v) : a < u < b, c < v < d }
in rectangular (i.e. Cartesian) coordinates a rectangle is a rectangle as
usual but in other coordinate systems it would be something of a different
shape (see figure).
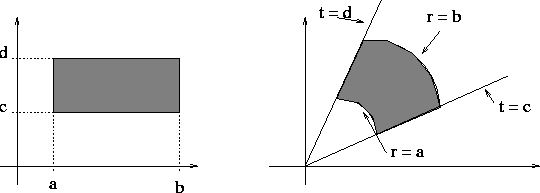 Notice that in rectangular coordinates, x=x0, y=y0 are the equations of a vertical and a horizontal straight lines but in polar coordinates, r=r0 is the equation of the circle centered at the origin of radius r0 and t=t0 is the equation of the half line (ray) from the origin straight out making an angle t0 with the x-axis.
Any integral can be computed by the limit of Riemann sums over cartesian
rectangles or Riemann sums over polar rectangles. The area of a cartesian
rectangle of sides dx and dy is dx*dy but the area of a polar rectangle
of sides dr and dt is NOT just dr*dt. Let's compute this area.
What we want is the area of the general polar rectangle obtained when
a |
> Area_of_sector := dt*(Pi*r^2)/(2*Pi);
2
Area_of_sector := 1/2 dt r
| hence, the element of area dA of a little general polar rectangle will be, |
> dA := b^2*dt/2 - a^2*dt/2;
2 2
dA := 1/2 b dt - 1/2 a dt
| this simplifies to, |
> dA :='(1/2)'* '(a+b)'*(b-a)*dt;
dA := 1/2 (a + b) (b - a) dt
| or using the definition of dr and calling r=(a+b)/2 we get, |
> dA := r*dr*dt;
dA := r dr dt
We can now write the following
Theorem: |
> ;
/ / / /
| | | |
| | f(x, y) dx dy = | | f(r cos(t), r sin(t)) r dt dr
| | | |
/ / / /
D D
| i.e. not only x and y need to be changed into r,t expressions but also the element of area dA which is dx*dy in rectangular coordinates changes into r*dt*dr in polar coordinates. Don't forget the extra r. |