Exercises on Double Integrals |
> Int(Int(x^4-y^2,x=1..2),y=0..1) = int(int(x^4-y^2,x=1..2),y=0..1);
1 2
/ /
| | 4 2 88
| | x - y dx dy = ----
| | 15
/ /
0 1
> Int(Int(sin(x+y),x=0..Pi/2),y=0..Pi/2)=
1/2 Pi 1/2 Pi 1/2 Pi
/ / /
| | |
| | sin(x + y) dx dy = | sin(y) + cos(y) dy
| | |
/ / /
0 0 0
| and this last integral is equal to: |
> Int(int(sin(x+y),x=0..Pi/2),y=0..Pi/2) =
> int(int(sin(x+y),x=0..Pi/2),y=0..Pi/2);
1/2 Pi
/
|
| sin(y) + cos(y) dy = 2
|
/
0
|
Double integrals can be used to compute volumes. Here are some examples.
|
Problem1:
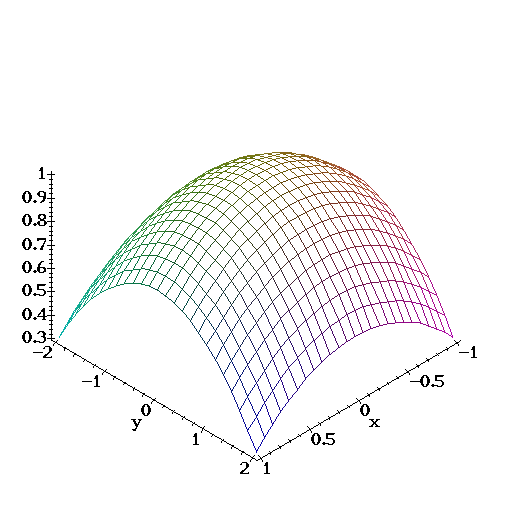
| Find the volume of the solid lying under the elliptic paraboloid |
> z := 1 - (x^2/4 + y^2/9);
2 2
z := 1 - 1/4 x - 1/9 y
|
and above the square R=[-1,1]x[-2,2]. The solid looks like this: |
> plot3d(z,x=-1..1,y=-2..2,axes=frame);
|
|
Solution1:
| Computing the integral over the square we get: |
> Int(Int(z,x=-1..1),y=-2..2) = int(int(z,x=-1..1),y=-2..2);
2 1
/ /
| | 2 2 166
| | 1 - 1/4 x - 1/9 y dx dy = ---
| | 27
/ /
-2 -1
| which is approximately, |
> ans1 := evalf(int(int(z,x=-1..1),y=-2..2),2);
ans1 := 6.1
|
|
Problem2:
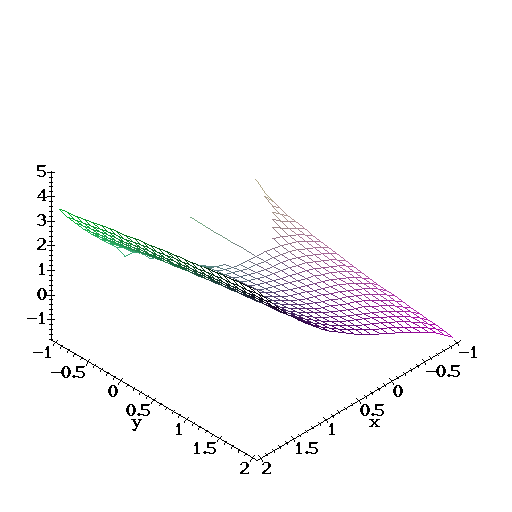
| Find the volume of the solid in the first octant bounded by the surface, |
> z2 := x*sqrt(x^2+y);
2 1/2
z2 := x (x + y)
|
and the planes x=1, and y=1.
|
Solution2:
| The double integral will compute the volume as the limit of approximations with blocks like the ones shown in the picture below: |
> with(mvcal):
> blockapp(z2,x=0..1,y=0..1);
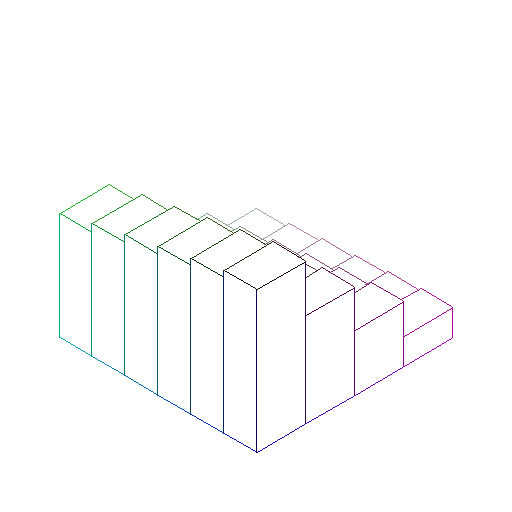
| The actual surface on the first octant looks like this, |
> plot3d(z2,x=-1..2,y=-1..2,axes=frame);
| Computing the double integral we get, |
> Int(Int(z2,x=0..1),y=0..1);
1 1
/ /
| | 2 1/2
| | x (x + y) dx dy
| |
/ /
0 0
| actually maple had a hard time with this integral in my computer. It refused to compute the exact expression for the integral eventhough a simple substitution (u=x2) does it. Any way after a lot of computing... |
> evalf(");
.4875805666
| If we do the integration over x by hand and let maple handle the integration over y we get the exact answer as, |
> ans2 := int((1+y)^(3/2)-y^(3/2),y=0..1)/3;
1/2
ans2 := 8/15 2 - 4/15
> evalf(");
.4875805663