|
Consider a smooth function of two variables: |
|
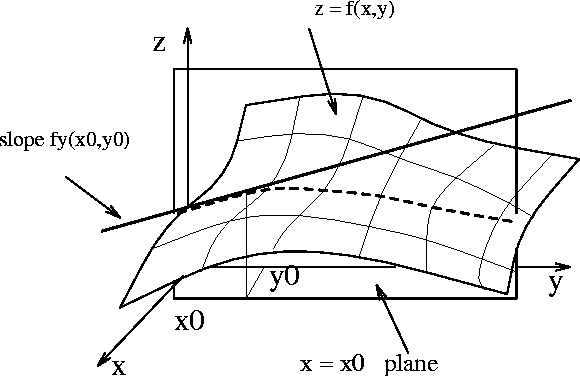
The partial derivative fy(x0,y0) is a special case of a directional derivative. It is the directional derivative in the direction of the unit vector "j".
If you imagine yourself standing on the surface at the point (x0,y0,z0)
and looking in the direction of "j" the slope you see is exactly the
value of fy(x0,y0). If you turn around and you now find yourself looking in
the direction of the unit vector "u" say, then the slope you see is
called the directional derivative in the direction of u.
Another way to look at it is to imagine the plane in the above figure revolving
around the axis through the point (x0,y0) (i.e. the line x=x0, y=y0). These
planes cut the surface at different curves (dashed curve in the figure). The
slope of the tangent at the point (x0,y0,z0) to this curve on the surface when
the plane contains the vector u=(a,b) attached to (x0,y0) is the directional
derivative in the direction of u. The algebraic definition of directional derivative is obtained if we think of f as a function of the vector r=(x,y). We have, |
> #
d f(r + h j) - f(r)
---- z = Limit -----------------
dy h -> 0 h
| the partial fy is the rate of change of f when r moves a bit from r in the direction of j. i.e. from r to r+hj. If we now let j be an arbitrary unit vector u, we get the formula for the directional derivative in the direction of u given by, |
> #
f(r + h u) - f(r)
Duf = Limit -----------------
h -> 0 h
| so the directional derivative of f in the direction of u, "Duf" is the rate of change of f when we move from r a little bit in the direction of u. i.e. from r to r+hu. in terms of the components we have, |
> #
f(x + h a, y + h b) - f(x, y)
Duf = Limit -----------------------------
h -> 0 h
| where we have assumed that u=(a,b). If we now let, |
> #
F(h) = f(x + h a, y + h b)
| we can see that the derivative of F at h=0 is, |
> #
d / F(h) - F(0)\
---- F(0) = |Limit -----------| = Duf
dh \h -> 0 h /
| but using the chain rule we obtain, |
> Duf = 'diff(f,x)'*a + 'diff(f,y)'*b;
/ d \ / d \
Duf = |---- f| a + |---- f| b
\ dx / \ dy /
| this last formula can be seen as the inner product between the so called gradient of f with the direction vector u=(a,b). The gradient of f is the vector of partial derivatives. Maple gives you this vector with the command, |
> grad(f(x,y),[x,y]);
d d
[ ---- f(x, y), ---- f(x, y) ]
dx dy
so the above can be stated as a, TheoremThe directional derivative of f in the direction of u=(a,b) is the projection of the gradient of f onto the direction u. Or in symbols, |
> Duf = innerprod( grad(f(x,y),[x,y]) , [a,b] );
/ d \ / d \
Duf = |---- f(x, y)| a + |---- f(x, y)| b
\ dx / \ dy /
|
The fact that Duf can be written as the innerprod of the gradient of f with u has a very important consequence. To see this remember the coordinate free definition of inner product. The inner product of two vectors, u and v say, is always equal to the length of u times the length of v times the cosine of the angle in between u and v. If we suppose that the angle between grad(f) and u is t, then, |
> #
Duf = | grad(f) | cos(t)
|
and since cos(t) is always in between 1 and -1 we have that, In other words at every point on the smooth surface the direction of grad(f) and -grad(f) at that point show where we need to look to find the directions of steepest ascend and steepest descent on the surface at that point. This fact can be exploited to find fast ways to climb surfaces (or functions of several variables). |