| Geometrically the existence of the derivative of a real valued function of a single real variable assures that the function behaves locally like a straight line. That is, when the derivative exists it is possible to approximate the function by its tangent line to a point if we don't move to far from that point. In other words if you know that the derivative of y=f(x) exits at x=a you know that if you zoom-in to around x=a ( for example with a magnifying glass) the function will start looking more and more like the straight line through the point (a,f(a)) with slope equal to the derivative of y=f(x) at x=a. |
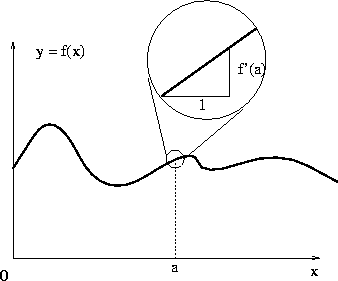
|
The 'meat' of the concept of derivative is in the fact that the original function can be approximated by a linear function around the point (a,f(a)).
All the information about the linear function that best approximates the
curve at (a,f(a)) is encoded in the point itself and the derivative
of f at x=a. If f is now a function not only of x, but of x and y, then the curve becomes the surface z=f(x,y) and the tangent line becomes the tangent plane to the surface. The concept of derivative stays put however. We say that the function of two variables x and y, is differentiable at x=a,y=b if when we zoom-in to the point (a,b,f(a,b)) on the surface the function looks more and more like a linear function (but now in two dimensions) i.e. it looks more and more like the tangent plane at the point. All the information about the tangent plane at a point of a surface is encoded in the point itself and the partial derivatives of f w.r.t. x and y at (a,b). If you don't remember this check the definition of the tangent plane. It is therefore natural to think of the vector of partial derivatives of f as the 'derivative' in higher dimensions. |