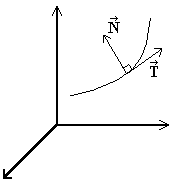
 v = dR/dt = dR/ds * ds/dt = T * ds/dt a = dv/dt = dT/dt * ds/dt + T * 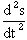 = = = dT/dt * (ds/dt)^2 + T * 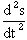 dT/ds = K*N, where K is the radius of curvature. a = K(ds/dt)^2 * N + 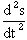 * T * Ta = aN * N + aT * T aN = K*(ds/dt)^2 = K |v|^2 = (|v|^2)/rho, where rho is the radius. aT = 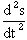 = d|v|/dt = d|v|/dtaN from above is the centripetal acceleration.
Example: 1
Example 2: |