Properties of Curves

Conclusion of Motion Along a Curve

What happens if we're dealing with a curve with a velocity of constant magnitude?
|v(t)| = v(t) . v(t) = C
Differentiating by the Product Rule:
(dv/dt).v + v.(dv/dt) = 0
2 * (dv/dt).v = 0
Since, (dv/dt) = a(t),
v.a = 0
A velocity of constant magnitude is always perpendicular to the acceleration.

Properties of Vector Curves

Distance Along a Curve

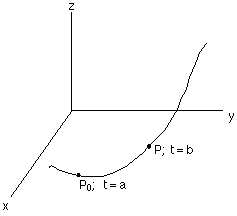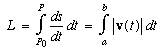
Example 1:
The Perimeter of a Circle:
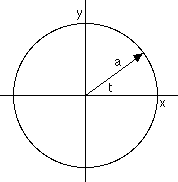x = a cos(t); y = a sin(t)
R = a cos t i + a sin t j
v = -a sin t i + a cos t j
|v| = a

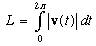
L= 2a*pi

Example 2:
Perimeter of an Ellipse:
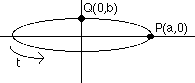x = a cos(t); y = b sin(t)
R = a cos t i + b sin t j
v = -a sin t i + b cos t j


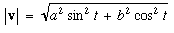
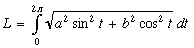
This form of integral is known as the elliptic integral. The elliptic integral has no elementary solutions, and thus the perimeter of an ellipse must be found on a case by case basis, using numerical techniques.

Tangents

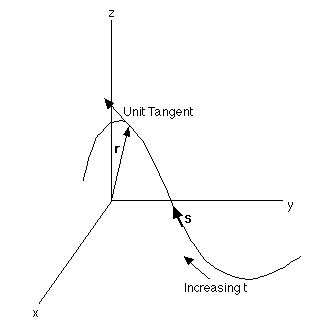
The unit tangent can be found by:
T = v(t) / |v(t)|
Also, (dR/ds) = (dR/dt) * (dt/ds) = v(t) / |v(t)| = T

Example:
Tangents of an Ellipse:

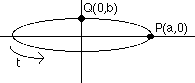
From above:
v = -a sin t i + b cos t j

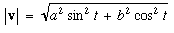
T = v(t) / |v(t)|
At P, t=0 and => T = j
At Q, t=pi/2 and => T = -i

Curvature

Curvature is normally represented by the Greek Symbol Kappa, but I'll use a capital K here. Similarly, the radius of curvature is represented by a Greek rho, I'll use a lowercase r.

_________ K=0, r is Infinite

K=1/a, r=a
At P, K is infinite and r=0.

The concept of curvature comes from fitting a circle tangent to the curve in at the point of question. When the circle fits just right, the radius of the circle is defined as the radius of curvature, r, and 1/r is the curvature, K.

For any curve, the curvature can be calculated using the following formula:
K = |(dT/ds)| = (|v x a|)/|v|^3
For a proof of the above equation, see Thomas & Finney, Calculus, 8th Edition, p 792.