Stokes Theorem

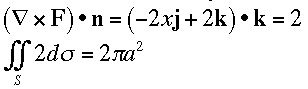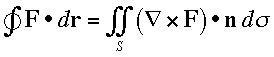
In Lecture 9 we talked about the divergence theorem. Lecture 10 moves on to the last of the three theorems of vector calculus which we will be discussing, Stokes Theorem. Stokes theorem deals with the problem of a 3-Dimensional curve in space, and the line integral around such a curve.

Stokes Theorem

Let C be any closed curve in 3D space, and let S be any surface bounded by C:

This is a fairly remarkable theorem, since S can be any surface bounded by the curve, and have just about any shape.

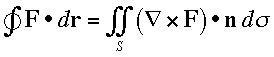
Stokes Theorem reduces to Green's Theorem when the curve is a 2-D curve, i.e. the curve lies in a plane.

Examples

Evaluate the flux of

xF across S, where F = -yi + xj + (x^2)k and the surface is

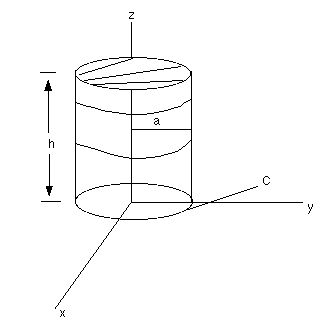
We can do this problem in three ways:

Do the surface integral directly.
Do a line integral through use of Stokes's theorem.
Compute the line integral in choice 2 by using another Stoke's Theorem surface.

First - #2, The Line Integral

C: r = a cos t i + a sin t j -- 0<=t<=2*pi
dr = T ds = T v dt = - a sint t i + a cos t j
on C: F = - a sin t i + a cos t j + a^2 cos^2 t k

Next - #1, The Direct Surface Integral

First we compute the curl of F:

Now, we do the surface integral dividing S into S1 = Top + S2 = Bottom

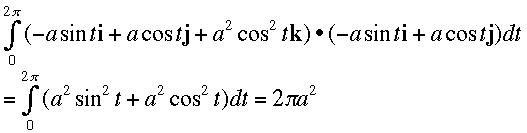
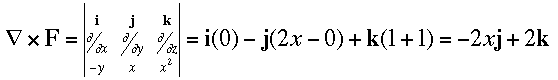
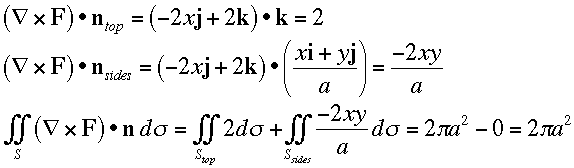
The zero on the sides integral comes from the symmetry of the integrand. xy is positive in Q 1 and 3, and negative in Q 2 and 4. Thus going all the way around the cylinder all these cancel out and the integral adds up to zero.

Last - #3, The Easy Surface Integral

We know that the flux of xF through S is equal to the line integral around C by Stoke's Theorem. Stokes Theorem says that we can do the line integral by computing the flux of xF through any surface bounded by C. So, we can use the circle in the plane of C as our surface.

Thus you can see what a powerful tool Stoke's Theorem is. Rather than do the integral directly (the hardest of the 3 choices) we can use either of 2 easier methods.

Lecture given by Prof. Alan Zehnder on 9/22/95
Lecture notes written by Lawrence C. Weintraub