The equation of a Plane through 3 given points A, B, C.
New [P3points.mp] Maple procedure using LinearAlgebra.
 |
> a := vector(3): b := vector(3): c:=vector(3):
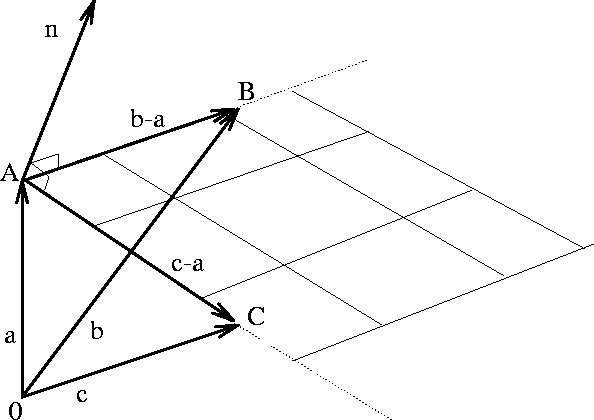
| The normal vector to the plane will be given by |
> n := crossprod(b-a,c-a);
n := [ (b[2] - a[2]) (c[3] - a[3]) - (b[3] - a[3]) (c[2] - a[2]),
(b[3] - a[3]) (c[1] - a[1]) - (b[1] - a[1]) (c[3] - a[3]),
(b[1] - a[1]) (c[2] - a[2]) - (b[2] - a[2]) (c[1] - a[1]) ]
| and to compute the equation of the plane we do |
> r := vector([x,y,z]):
> innerprod(n, r-a);
- b[2] a[3] x - a[2] c[3] x + b[2] c[3] x + b[3] a[2] x + a[3] c[2] x
- b[3] c[2] x + a[1] c[3] y + b[1] a[3] y - a[3] c[1] y - b[1] c[3] y
+ b[3] c[1] y - b[3] a[1] y - b[2] c[1] z + b[1] c[2] z - b[1] a[2] z
- a[1] c[2] z + b[2] a[1] z + a[2] c[1] z - b[2] c[3] a[1]
+ b[1] c[3] a[2] + b[3] c[2] a[1] + b[2] c[1] a[3] - b[1] c[2] a[3]
- b[3] c[1] a[2]
| In order to "collect" terms in x, y and z we write, |
> collect(",[x,y,z]);
(b[2] c[3] - b[2] a[3] - a[2] c[3] - b[3] c[2] + b[3] a[2] + a[3] c[2]) x
+ (b[3] c[1] - b[3] a[1] - a[3] c[1] - b[1] c[3] + b[1] a[3] + a[1] c[3]) y
+ (b[1] c[2] - b[1] a[2] - a[1] c[2] - b[2] c[1] + b[2] a[1] + a[2] c[1]) z
- b[2] c[3] a[1] - b[1] c[2] a[3] + b[1] c[3] a[2] + b[2] c[1] a[3]
+ b[3] c[2] a[1] - b[3] c[1] a[2]
| The equation of the plane is then given by the previous expression = 0. It is more convenient to pack the above commands into a maple procedure as follows: |
> P3points := proc(a,b,c)
> local ex1,ex2,n,_x,_y,_z,r;
> n := crossprod(b-a,c-a);
> r := vector([_x,_y,_z]);
> ex1 := innerprod(n,r-a);
> ex2 := collect(ex1,[_x,_y,_z]);
> ex2 = 0
> end;
| Let's test it, |
> P3points([0,0,-8],[0,4,0],[8,0,0]);
32 _x + 64 _y - 32 _z - 256 = 0
| OK this is the answer but to show how you can use maple to re-organize the way an equation looks we load the very useful "isolate" command with, |
> readlib(isolate):
> isolate(P3points([0,0,-8],[0,4,0],[8,0,0]),- 256);
-256 = - 32 _x - 64 _y + 32 _z
| Do you see how -256 was isolated on the right? We can also divide the whole equation through by 32 with, |
> "/32;
-8 = - _x - 2 _y + _z
| and now let's flip the rhs and lhs with, |
> isolate(",rhs("));
- _x - 2 _y + _z = -8
| Multiply through by (-1).... |
> "*(-1);
_x + 2 _y - _z = 8
| one more example, |
> P3points([1,1,-2],[-1,1,0],[0,2,2]);
- 2 _x - 8 + 6 _y - 2 _z = 0
1/4 _x + 1 - 3/4 _y + 1/4 _z = 0
| sorry I just wanted to divide by (-2), but not a big deal... just do |
> "*4;
_x + 4 - 3 _y + _z = 0
4 = - _x + 3 _y - _z
| and flip it around... |
> isolate(",rhs("));
- _x + 3 _y - _z = 4