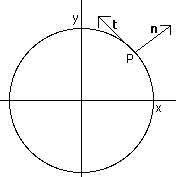
Last lecture left off discussing the "marriage" of vectors and calculus in order to find a vector tangent to a given curve in the x-y plane. The following example illustarates exactly how this can be done.

• 3-D Cartesian Coordinates

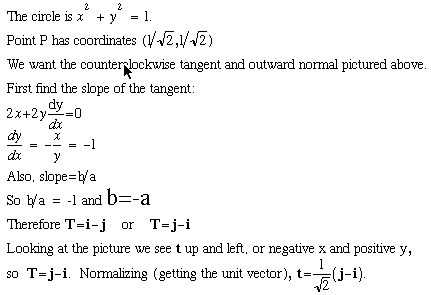
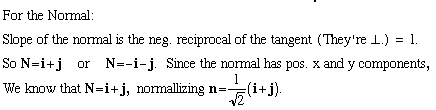
  In three dimensions, the two dimentional concepts are extended, with the simple addition of a third component- the unit vector parallel to the z axis, k.

  Magnitude and direction are still computed in extremely similar ways.

  

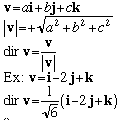
  We would still like to have angles to describe direction rather than a difficult to grasp set of components. Two Dimentions required one angle to define a direction. In three dimensions we'll need two.

• Spherical Coordinates

  Spherical coordinates define a vector in terms of its length (R), an angle between the vector and the z-axis (phi), and the angle between the vectors projection onto the xy plane and the x-axis (theta). [See picture below].

  

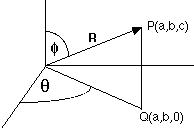
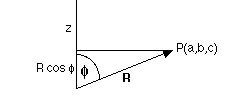
  By looking at the right triangles formed by the vector, its projection, and the axes, the relationship between the Spherical coordinates and Cartesian ones can be determined. It turns out that x = R sin (phi) cos (theta); y = R sin (phi) sin (theta); and z = R cos (phi).

  

• 3D Geometry In three dimentions there are four types of objects that can appear:
  1. Surfaces: Surfaces are of the form f(x,y,z) = 0 and are things like spherical shells or planes. Ex: x*x + y*y + z*z = 1 [sphere] or ax + by + cz = d [plane].
  2. Lines: A line is the intersection of two surfaces and is thus defined by a system of two equations, namely, f1(x,y,z)=0; f2(x,y,z)=0 Ex: x=2; y=3.
  3. Volume: Volumes are of the form f(x,y,z) << 0. Examples include things like a solid sphere x*x + y*y + z*z << 1.
  4. Point: (1,2,3).

• Identify the following sets of points (in 3D)

  1. 

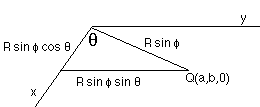
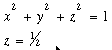
     The first equation is that of a sphere, while the second is that of a horizontal plane. The plane cuts the sphere parallel to the xy plane creating an intersection set of a circle. This is pictured below (Generated by Mathematica).

     

     ---

  2. 

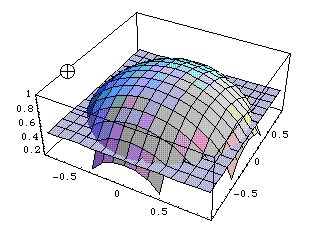
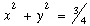
     This equation is the mathematical solution of the first set of equations, but it behaves very differently. Because z is not specified here, it can be anything and the result is the cylinder pictured below, which has its axis on the z axis and a radius of .866 (Generated by Mathematica).